Back to Compression and shear	Based on part of the GeotechniCAL reference package by Prof. John Atkinson, City University, London

• Change of size: bulk modulus
• Change of shape: shear modulus
• Uniaxial loading: Young's modulus and Poisson's ratio
• Relationships between stiffness moduli

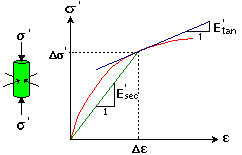As stresses are increased or decreased a material body will tend to change size and shape as strains occur: stiffness is the relationship between changes of stress and changes of strain.

The stiffness E' is the gradient of the stress-strain curve. Stiffnesses may be described by

a tangent modulus E'_tan = ds' / de

or by a secant modulus E'_sec = Ds' / De

Note: If the material is linearly elastic the stress-strain curve is a straight line and E'_tan = E'_sec.

Change of size: bulk modulus

Back to Stiffness

As the mean stress increases materials compress (reduce in volume). The bulk modulus K' relates the change in stress to the volumetric strain.

K'=	ds'mean
	de'v

where

s'_mean = (s'_x + s'_y + s'_z) / 3

Note:

In soils volumetric strains are due to changes of effective stress.

As the shear stress increases materials distort (change shape). The shear modulus G' relates the change in shear stress to the shear strain.

G =	dt
	dg

Sinse water has no shear strength, the value of the shar modulus, G, remains the same, independant of whether the loading process is drained or undrained.

• Typical values of E

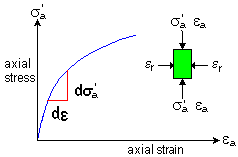Young's modulus and Poisson's ratio are measured directly in uniaxial compression or extension tests, i.e. tests with constant (or zero) stress on the vertical surfaces.
i.e. ds'_r = 0

Young's modulus

Poisson's ratio   n' = - de_r / de_a

Note:
If the material is incompressible, e_v = 0 and Poisson’s ratio, n = 0.5.
Uniaxial compression is the only test in which it is possible to measure Poisson's ratio with any degree of simplicity.

These are a function of the stress level, and the loading history, however a range is given below.

In bodies of elastic material the three stiffness moduli (E', K' and G') are related to each other and to Poisson’s ratio (n'). It assumed that the material is elastic and isotropic (i.e. linear stiffness is equal in all directions). The following relationships can be demonstrated (for proofs refer to a text on the strength of materials).

G' = E' / 2(1 + n')

K' = E' / 3(1 - 2n')

• Elasticity
• Perfect plasticity
• Elasto-plasticity

The stress-strain curve has features which are characteristic of different aspects of material behaviour and which are represented by different theories.

Shear modulus G = dt / dg Bulk modulus K' = ds'mean / dev or Young’s modulus E' = ds'a / dea (where ds'r = 0) Poisson’s ratio n' = - der / dea   (where ds'r = 0)

• Yield
• Normality

OA - rigid

AB - plastic

During perfectly plastic straining, plastic strains continue indefinitely at constant stress. The ratio of plastic strains is related to the yield stress, which also represents the failure stress.

Yield	Back to Perfect plasticity
Yield stress is the stress at the end of elastic behaviour (in a perfectly plastic material this is the same as the failure stress). In a 2-dimensional stress system the combination of yield stresses forms a yield curve, inside which failure can not occur.

The relationship between the ratio of plastic strains is such that the plastic strain vector is normal to the yield curve.

Normality is also known as associated flow.

There are simultaneous elastic and plastic strains and the plastic strains cause the yield stress to change. There are two cases which are typically found: 

Strain hardening The plastic strain dep causes an increase in the yield stress. The hardening law is ds'yield / dep Soils with loosely packed grains are strain hardening because the disturbance during sharing causes the grains to move closer together.
Strain softening The plastic strain dep causes a decrease in the yield stress. Soils with densely packed grains are strain softening because disturbance during sharing causes the grains to move apart causing dilation.

For relatively low ~ medium risk projects, an assumption may be made that the stress - strain response can be represented by two straight lines, to describe an initial linear elastic stiffness (OA) and the yield stress or strength at failure during plastic straining (AB).