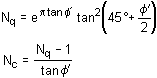
The ultimate bearing capacity (qf) is the value of bearing stress which causes a sudden catastrophic settlement of the foundation (due to shear failure).
The allowable bearing capacity (qa) is the maximum bearing stress that can be applied to the foundation such that it is safe against instability due to shear failure and the maximum tolerable settlement is not exceeded. The allowable bearing capacity is normally calculated from the ultimate bearing capacity using a factor of safety (Fs).
When excavating for a foundation, the stress at founding level is relieved
by the removal of the weight of soil. The net bearing pressure (qn)
is the increase in stress on the soil.
qn = q - qo
qo = g D
where D is the founding depth and g is the
unit weight of the soil removed.
Failure mechanisms and derivation of equations | Bearing capacity |
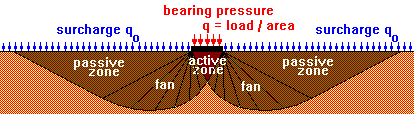
qf = (2 + p) su = 5.14 suThis equation is based on a weightless soil. Therefore if the soil is non-cohesive (c=0) the bearing capacity depends on the surcharge qo. For a footing founded at depth D below the surface, the surcharge qo = gD. Normally for a shallow foundation (D<B), the shear strength of the soil between the surface and the founding depth D is neglected.
radius of the fan r = r0 .exp[q.tanf'].
q is the fan angle in radians (between 0 and p/2)
f' is the angle of friction of the soil
ro = B/[2 cos(45+f'/2)]
Upper and lower bound solutions | Failure mechanisms and derivation of equations |
The ultimate load capacity of a footing can be estimated by assuming a failure mechanism and then applying the laws of statics to that mechanism. As the mechanisms considered in an upper bound solution are progressively refined, the calculated collapse load decreases.
As more stress regions are considered in a lower bound solution, the calculated collapse load increases.
Therefore, by progressive refinement of the upper and lower bound solutions,
the exact solution can be approached. For example, Terzaghi's mechanism
gives the exact solution for a strip footing.
Semi-circular slip mechanism | Failure mechanisms and derivation of equations |
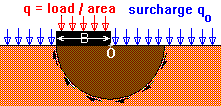Suppose the mechanism
is assumed to have a semi-circular slip surface. In this case, failure
will cause a rotation about point O. Any surcharge qo will resist
rotation, so the net pressure (q - qo) is used. Using the equations
of statics:
Circular arc slip mechanism | Failure mechanisms and derivation of equations |
Consider a slip
surface which is an arc in cross section, centred above one edge of the
base. Failure will cause a rotation about point O. Any surcharge qo
will resist rotation so the net pressure (q - qo) is used. Using
the equations of statics:
Bearing capacity of shallow foundations | Bearing capacity |
For drained loading, calculations are in terms of effective stresses;
f´
is > 0 and N
c, Nq and Ng
are all > 0.
For undrained loading, calculations are in terms of total stresses;
the undrained shear strength (su); Nq = 1.0 and Ng
= 0
c = apparent cohesion intercept
qo = g . D (i.e. density x depth)
D = founding depth
B = breadth of foundation
g = unit weight of the soil removed.
Bearing capacity equation (undrained) | Bearing capacity of shallow foundations |
Bearing capacity equation (drained) | Bearing capacity of shallow foundations |
qf =c.Nc +qo.Nq + ½g.B .NgThis equation is applicable only for shallow footings carrying vertical non-eccentric loading.
qf = c .Nc .sc + qo .Nq .sq + ½ g .B .Ng .sgOther factors can be used to accommodate depth, inclination of loading, eccentricity of loading, inclination of base and ground. Depth is only significant if it exceeds the breadth.
Bearing capacity factors | Bearing capacity equation (drained) |
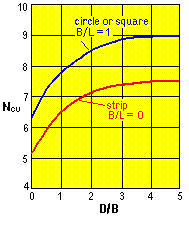
Exact values for Ng are not directly obtainable; values have been proposed by Brinch Hansen (1968), which are widely used in Europe, and also by Meyerhof (1963), which have been adopted in North America.
Shape factors | Bearing capacity equation (drained) |
|
|
|
|
|
| square |
|
|
|
| circle |
|
|
|
| rectangle (B<L) | 1+ 0.2(B/L) | 1+ 0.2(B/L) | 1 - 0.4(B/L) |
Depth factors | Bearing capacity equation (drained) |
Factor of safety | Bearing capacity of shallow foundations |
The factor of safety should be applied only to the increase in stress, i.e. the net bearing pressure qn. Calculating qa from qf only satisfies the criterion of safety against shear failure. However, a value for Fs of 2.5 - 3.0 is sufficiently high to empirically limit settlement. It is for this reason that the factors of safety used in foundation design are higher than in other areas of geotechnical design. (For slopes, the factor of safety would typically be 1.3 - 1.4).
Experience has shown that the settlement of a typical foundation on
soft clay is likely to be acceptable if a factor of 2.5 is used. Settlements
on stiff clay may be quite large even though ultimate bearing capacity
is relatively high, and so it may be appropriate to use a factor nearer
3.0.
Presumed bearing values | Bearing capacity |
| Category | Types of rocks and soils | Presumed bearing value |
| Non-cohesive soils | Dense gravel or dense sand and gravel | >600 kN/m² |
| Medium dense gravel,
or medium dense sand and gravel |
<200 to 600 kN/m² | |
| Loose gravel, or loose sand and gravel | <200 kN/m² | |
| Compact sand | >300 kN/m² | |
| Medium dense sand | 100 to 300 kN/m² | |
| Loose sand | <100 kN/m² depends on
degree of looseness |
|
| Cohesive soils | Very stiff bolder clays & hard clays | 300 to 600 kN/m² |
| Stiff clays | 150 to 300 kN/m² | |
| Firm clay | 75 to 150 kN/m² | |
| Soft clays and silts | < 75 kN/m² | |
| Very soft clay | Not applicable | |
| Peat | Not applicable | |
| Made ground | Not applicable |
Presumed bearing values for Keuper Marl
| Weathering | Zone | Description | Presumed bearing value |
| Fully weathered | IVb | Matrix only | as cohesive soil |
| Partially weathered | IVa | Matrix with occasional pellets less than 3mm | 125 to 250 kN/m² |
| III | Matrix with lithorelitics up to 25mm | 250 to 500 kN/m² | |
| II | Angular blocks of unweathered marl with virtually no matrix | 500 to 750 kN/m² | |
| Unweathered | 1 | Mudstone (often not fissured) | 750 to 1000 kN/m² |
Bearing capacity of piles | Bearing capacity |
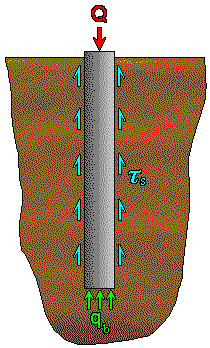The ultimate bearing
capacity of a pile used in design may be one three values:
For large-diameter piles, settlement can be large, therefore a safety factor of 2-2.5 is usually used on the working load.
Full shaft capacity is mobilised at much smaller displacements than
those related to full base resistance. This is important when determining
the settlement response of a pile. The same overall bearing capacity may
be achieved with a variety of combinations of pile diameter and length.
However, a long slender pile may be shown to be more efficient than a short
stubby pile. Longer piles generate a larger proportion of their full capacity
by skin friction and so their full capacity can be mobilised at much lower
settlements.
The proportions of capacity contributed by skin friction and end bearing
do not just depend on the geometry of the pile. The type of construction
and the sequence of soil layers are important factors.
Driven piles in non-cohesive soil | Bearing capacity of piles |
In non-cohesive soils, skin friction is low because a low friction 'shell' forms around the pile. Tapered piles overcome this problem since the soil is recompacted on each blow and this gap cannot develop.
Pile capacity can be calculated using soil properties obtained from standard penetration tests or cone penetration tests. The ultimate load must then be divided by a factor of safety to obtain a working load. This factor of safety depends on the maximum tolerable settlement, which in turn depends on both the pile diameter and soil compressibility. For example, a safety factor of 2.5 will usually ensure a pile of diameter less than 600mm in a non-cohesive soil will not settle by more than 15mm.
Although the method of installing a pile has a significant effect on
failure load, there are no reliable calculation methods available for quantifying
any effect. Judgement is therefore left to the experience of the engineer.
Ultimate pile capacity | Driven piles in non-cohesive soil |
Values of Ks and d can be
related to the angle of internal friction (f´)
using the following table according to Broms.
| Material | d | Ks | |
|---|---|---|---|
| low density | high density | ||
| steel | 20° | 0.5 |
1.0 |
| concrete | 3/4 f´ | 1.0 | 2.0 |
| timber | 2/3 f´ | 1.5 | 4.0 |
It must be noted that, like much of pile design, this is an empirical relationship. Also, from empirical methods it is clear that Qs and Qb both reach peak values somewhere at a depth between 10 and 20 diameters.
It is usually assumed that skin friction never
exceeds 110 kN/m² and base resistance will not exceed 11000 kN/m².
Standard penetration test | Driven piles in non-cohesive soil |
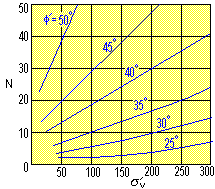The standard penetration
test is a simple in-situ test in which the N-value is the mumber of blows
taken to drive a 50mm diameter bar 300mm into the base of a bore hole.
Schmertmann (1975) has correlated N-values obtained from SPT tests against
effective overburden stress as shown in the figure.
The effective overburden stress = the
weight of material above the base of the borehole - the wight of water
e.g. depth of soil = 5m, depth of water =
4m, unit weight of soil = 20kN/m³,
s'v
= 5m x 20kN/m³ - 4m x 9.81kN/m³ »
60 kN/m²
Once a value for f´ has been estimated, bearing capacity factors can be determined and used in the usual way.
Meyerhof (1976) produced correlations between base and frictional resistances and N-values. It is recommended that N-values first be normalised with respect to effective overburden stress:
Normalised N = Nmeasured x 0.77 log(1920/s´v)
| Pile type | Soil type | Ultimate base resistance
|
Ultimate shaft resistance
|
| Driven | Gravelly sand
Sand |
but < 400 N |
|
| Sandy silt
Silt |
but < 300 N |
||
| Bored | Gravel and sands |
but < 300 N |
Navg |
| Sandy silt
Silt |
but < 300 N |
L = embedded length
d = shaft diameter
Navg = average value along shaft
Cone penetration test | Driven piles in non-cohesive soil |
qb = average cone resistance calculated over a depth equal to three pile diameters above to one pile diameter below the base level of the pile.Shaft resistance
| Type of pile |
|
| Solid timber )
Pre-cast concrete ) Solid steel driven ) |
0.005 - 0.012 |
| Open-ended steel | 0.003 - 0.008 |
Bored piles in non-cohesive soil | Bearing capacity of piles |
Driven piles in cohesive soil | Bearing capacity of piles |
For piles driven into stiff clays, a little consolidation takes place, the soil cracks and is heaved up. Lateral vibration of the shaft from each blow of the hammer forms an enlarged hole, which can then fill with groundwater or extruded porewater. This, and 'strain softening', which occurs due to the large strains in the clay as the pile is advanced, lead to a considerable reduction in skin friction compared with the undisturbed shear strength (su) of the clay. To account for this in design calculations an adhesion factor, a, is introduced. Values of a can be found from empirical data previously recorded. A maximum value (for stiff clays) of 0.45 is recommended.
The ultimate bearing capacity Qf of a driven pile in cohesive
soil can be calculated from:
Qf = Qb + Qs
where the skin friction term is a summation of layer resistances
Qs = S( a
.su(avg) .As)
and the end bearing term is
Qb = su .Nc .Ab
Nc = 9.0 for clays and silty clays.
Bored piles in cohesive soil | Bearing capacity of piles |
The mobilisation of full end-bearing capacity by large-diameter piles
requires much larger displacements than are required to mobilise full skin-friction,
and therefore safety factors of 2.5 to 3.0 may be required to avoid excessive
settlement at working load.
Carrying capacity of piles in layered soil | Bearing capacity of piles |
The base resistance at the pile toe is
qp = q2 + (q1 -q2)H / 10B
but
£ q1
where B is the diameter of the pile, H is the thickness between the base of the pile and the top of the weaker layer, q2 is the ultimate base resistance in the weak layer, q1 is the ultimate base resistance in the strong layer.
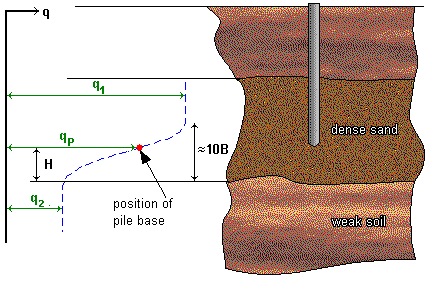
Effects of groundwater | Bearing capacity of piles |
Effect on bearing capacity
In cohesive soils, the permeability is so low that any movement of
water is very slow. They do not suffer any reduction in bearing capacity
in the presence of groundwater.
In granular soils, the position of the water table is important. Effective
stresses in saturated sands can be as much as 50% lower than in dry sand;
this affects both the end-bearing and skin-friction capacity of the pile.
Effects on construction
When a concrete cast-in-place pile is being installed and the bottom
of the borehole is below the water table, and there is water in the borehole,
a 'tremie' is used.
With its lower
end lowered to the bottom of the borehole, the tremmie is filled with concrete
and then slowly raised, allowing concrete to flow from the bottom. As the
tremie is raised during the concreting it must be kept below the surface
of the concrete in the pile. Before the tremie is withdrawn completely
sufficient concrete should be placed to displace all the free water and
watery cement. If a tremie is not used and more than a few centimetres
of water lie in the bottom of the borehole, separation of the concrete
can take place within the pile, leading to a significant reduction in capacity.
A problem can also arise when boring takes place through clays. Site investigations may show that a pile should terminate in a layer of clay. However, due to natural variations in bed levels, there is a risk of boring extending into underlying strata. Unlike the clay, the underlying beds may be permeable and will probably be under a considerable head of water. The 'tapping' of such aquifers can be the cause of difficulties during construction.
Effects on piles in service
The presence of groundwater may lead to corrosion or deterioration
of the pile's fabric.
In the case of steel piles, a mixture of water and air in the
soil provides conditions in which oxidation corrosion of steel can occur;
the presence of normally occurring salts in groundwater may accelerate
the process.
In the case of concrete piles, the presence of salts such as
sulphates or chlorides can result in corrosion of reinforcement, with possible
consequential bursting of the concrete. Therefore, adequate cover must
be provided to the reinforcement, or the reinforcement itself must be protected
in some way. Sulphate attack on the cement compounds in concrete may lead
to the expansion and subsequent cracking. Corrosion problems are minimised
if the concrete has a high cement/aggregate ratio and is well compacted
during placement.
