Piled foundations

Adapted from the Foundation section of the GeotechniCAL Reference Manual Author: David Toll (Durham Univ.)

Piles generally used because adequate bearing capacity can not be found at shallow enough depths to support the structural loads. It is important to understand that piles get support from both end bearing and skin friction. The proportion of carrying capacity generated by either end bearing or skin friction depends on the soil conditions. Piles can be used to support various different types of structural loads.

Types of piles

End bearing piles
Friction piles
Settlement reducing piles
Tension piles
Laterally loaded piles

Pile construction

Soil auger use to form a non-displacement pile

Displacement piles

soil is displaced radially as well as vertically as the pile shaft is driven or jacked into the ground

Non-displacement (or replacement) piles

soil is removed and the resulting hole filled with concrete or a precast concrete pile is dropped into the hole and grouted in.

Choice of pile Depends on:

Location and type of structure
Ground conditions
Durability
Cost

Pile groups

Piles are frequently installed in groups.
A pile group must be considered as a composite block of piles and soil, and not a multiple set of single piles.
The capacity of each pile may be affected by the driving of subsequent piles in close proximity.
Compaction of the soil between adjacent piles is likely to lead to higher contact stresses and thus higher shaft capacities for those piles.
The ultimate capacity of a pile group is not always dependent on the individual capacity of each pile.
When analysing the capacity of a pile group 3 modes of failure must be considered:

Single pile failure.
Failure of rows of piles.
Block failure.

Ultimate Bearing Capacity

The ultimate bearing capacity may be take as one of three values:

the maximum load Q_max, at which further penetration occurs without the load increasing
a calculated value Q_f given by the sum of the end-bearing and shaft resistances
or the load at which a settlement of 0.1 diameter occurs (when Q_max is not clear).

For large-diameter piles, settlement can be large, therefore a safety factor of 2-2.5 is usually used on the working load.

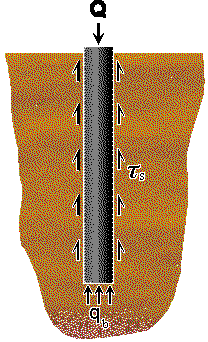
A pile loaded axially will carry the load partly by shear stresses, t_s, generated along the shaft of the pile and partly by normal stresses, q_b, generated at the base.

The ultimate capacity Q_f of a pile is equal to the base capacity plus the skin friction acting on the shaft.

Q_f =	Q_b	+	Q_s
=	A_b . q_b	+	å (A_s . t_s)

where

A_b is the area of the base
A_s is the surface area of the shaft within a soil layer.

The Greek letter S is used to indicate that it may be appropriate to add together the skin friciton generated by each layer of soil which the pile enters.

The proportions of capacity contributed by skin friction and end bearing do not depend on the geometry of the pile alone. The type of construction and the sequence of soil layers are important factors.

Settlement

Full shaft capacity is mobilised at much smaller displacements than those related to full base resistance. This is important when determining the settlement response of a pile. The same overall bearing capacity may be achieved with a variety of combinations of pile diameter and length. However, a long slender pile may be more efficient than a short stubby pile. Longer piles generate a larger proportion of their full capacity by skin friction and so their full capacity can be mobilised at much lower settlements.

Driven piles in non-cohesive soil

The base resistance, Q_b can be found from Terzaghi's equation for bearing capacity,

q_f= 1.3 c.N_c + q_o.N_q + 0.4 g.B.N_g

The 0.4g.B.N_g term may be ignored, since the diameter is considerably less than the depth of the pile.
The 1.3c.N_c term is zero, since the soil is non-cohesive (c=0).

The net unit base resistance is therefore q_nf = q_f - q_o = q_o (N_q -1)

and the net total base resistance is Q_b = q_o (N_q -1) A_b

The ultimate unit skin friction (shaft) resistance

q_s = K_s .s'_v . tand

where	s'_v	= average vertical effective stress in a given layer
	d	= angle of wall friction, based on pile material and f´
	K_s	= earth pressure coefficient

In layered soil the total skin friction resistance is given by the sum of the layer resistances: Q_s = S(K_s .s'_v .tand .A_s) The self-weight of the pile may be ignored, since the weight of the concrete is almost equal to the weight of the soil displaced. Therefore, the ultimate pile capacity is:

Q_f= A_b q_o N_q + S(K_s .s'_v .tand .A_s)

Calculate N_c, N_q and N_g

Values of K_s and d can be related to the angle of internal friction (f´)

using the following table according to Broms.

Material d K_s

low density high density

steel 20° 0.5 1.0

concrete ¾ f´ 1.0 2.0

timber ²/3; f´ 1.5 4.0

Like much of pile design, this is an empirical relationship.
From empirical methods it is clear that Q_s and Q_b both reach peak values at a depth of between 10 and 20 diameters.
It is usually assumed that skin friction never exceeds 110kN/m² and base resistance will not exceed 11000kN/m².

Driven piles in cohesive soil

Driving piles into clays alters the physical characteristics of the soil.

In soft clays, driving piles results in an increase in pore water pressure, u, causing a reduction in effective stress. Ground heave also occurs. As the pore water pressure dissipates with time and the ground subsides, the effective stress in the soil will increase. The increase in effective stress (s' = s - u) leads to an increase in the bearing capacity of the pile with time. In most cases, 75% of the ultimate bearing capacity is achieved within 30 days of driving.

For piles driven into stiff clays, a little consolidation takes place, the soil cracks and is heaved up. Lateral vibration of the shaft from each blow of the hammer forms an enlarged hole, which can then fill with groundwater or extruded porewater. This, and 'strain softening', which occurs due to the large strains in the clay as the pile is advanced, lead to a considerable reduction in skin friction compared with the undrained shear strength, s_u, of the clay. To account for this in design calculations an adhesion factor, a, is introduced. Values of a can be found from empirical data previously recorded. A maximum value (for stiff clays) of 0.45 is recommended.

The undrained shear strength, s_u, frequently increases with depth. The value used to calculate the end bearing capacity, Q_b, should be that at the base of the pile. The value used to calculate the shaft capacity, Q_s, should be the average value, s_u(avg), take at mid height.

Q_s = a .s_u(avg) .A_s
Q_b = s_u .N_c .A_b

N_c = 9.0 for clays and silty clays.

Bored piles in non-cohesive soil

The design process for bored piles in granular soils is essentially the same as that for driven piles. It must be assumed that boring loosens the soil and therefore, however dense the soil, the value of the angle of friction used for calculating N_q values for end bearing and d values for skin friction must be those assumed for loose soil. However, if rotary drilling is carried out under a bentonite slurry f' can be taken as that for the undisturbed soil.

Bored piles in cohesive soil

Following research into bored cast-in-place piles in London clay, calculation of the ultimate bearing capacity for bored piles can be done the same way as for driven piles. The adhesion factor should be taken as 0.45. It is thought that only half the undisturbed shear strength is mobilised by the pile due to the combined effect of swelling, and hence softening, of the clay in the walls of the borehole. Softening results from seepage of water from fissures in the clay and from the unset concrete, and also from 'work softening' during the boring operation.

Material	d	K_s
		low density	high density
steel	20°	0.5	1.0
concrete	¾ f´	1.0	2.0
timber	²/3; f´	1.5	4.0