Back to Soil Mechanics
by Prof. John Atkinson , City University, London
Back to Soil Mechanics |
Based on part of the GeotechniCAL
reference package by Prof. John Atkinson , City University, London |
The relationship
between volume change and effective stress is called compression and swelling.
(Consolidation and compaction are different.) The volume of soil grains
remains constant, so change in volume is due to change in volume of water.
Compression and swelling results from drained loading and the pore pressure remains constant. If saturated soil is loaded undrained there will be no volume change.
Back to Compression and swelling
| rearrangement of grains |  |
| fracture and rearrangement of grains |  |
| distortion or bending of grains |  |
On unloading, grains will not unfracture or un-rearrange, so volume change on unloading and
reloading (swelling and recompression) will be much less than volume change on first loading (compression).
In compression, soil behaviour is:
Back to Compression and swelling
Isotropic:
Equal stress in all directions. Applicable to triaxial test before
shearing.
p' = (s'a + 2s'r)
/ 3
= mean stress
ev = DV
/ Vo
= volumetric strain
One-dimensional:
Horizontal strains are zero. Applicable to oedometer test and in the
ground below wide foundations, embankments and excavations.
s'z = vertical stress
ev = DV
/ Vo
= DH / Ho
= De / (1+eo)
= volumetric strain
Back to Compression and swelling
Isotropic
compression and swelling is applied at the start of a triaxial test.
p' = (s'a + 2s'r)
/ 3
= mean stress
V = Vo - DVw
= volume
ev = DV
/ Vo = Dv / vo
= volumetric strain
v = V / Vs
= specific volume
As the mean
stress p' is raised and lowered there are volumetric strains and the specific
volume changes.
p'o = initial mean stress
vo = initial specific volume
Note the paths of compression, swelling and re-loading.
Back to Isotropic compression and swelling
For isotropic
compression and swelling there are simple relationships
First loading
normal compression line
OAD on the graph
v = N - l ln p'
Unloading and reloading
swelling line
BC on the graph
v = vk - k ln p'
N, l and k are
soil parameters.
vk and p'y locate the particular swelling line.
p'y is referred to as the yield stress.
If the current stress and the history of loading/unloading are known,
the current specific volume can be calculated.
Back to Equations for isotropic compression
Isotropic compression
can be represented by a bulk modulus K' or by the slope of the normal compression
line l (or the slope of a swelling line k):
these are related.
K' = dp' / dev
v = N - l ln p'
dv / v = - l dp' / vp'
Hence K' = vp' / l (or vp' / k )
Bulk modulus K' depends on v and p'. Both of these will change during
compression or swelling and so K' is not a soil constant.
Back to Equations for isotropic compression
| Typical values | wL | Ip | l |
| very high plasticity clay | 80 | 50 | 0.29 |
| high plasticity clay | 60 | 34 | 0.20 |
| intermediate plasticity clay | 42 | 23 | 0.14 |
| low plasticity clay | 30 | 12 | 0.07 |
| quartz sand | 0.15 | ||
| carbonate sand | 0.34 |
For clays l »
Ip / 170.
k / l is relatively
large (e.g. 0.25 - 0.35) because clay particles can bend and distort.
For sands l is relatively large due
to particles crushing (but states only reach NCL at high pressure).
k / l is relatively
small (e.g. 0.1) because sand particles crush and rearrange during first
compression.
Back to Isotropic compression and swelling
If the current state of soil is on
the normal compression line it is said to be normally consolidated.
If the soil is unloaded it becomes overconsolidated.
(Soil cannot usually be at a state outside the normal compression line unless it is bonded or structured).
At a state A the overconsolidation ratio is
Rp = p'y / p'a
(on NCL Rp = 1.0 and soil is normally consolidated).
Note: p'y is the point of intersection of the swelling line
through A and the NCL. This is usually close to the maximum past stress.
Back to Isotropic compression and swelling
The current state
of a soil is described by the stress p', the specific volume v and the
overconsolidation ratio Rp (for a complete description the shear
stress q' is required).
The state at A is given by any two of
va , p'a , Rp = p'y / p'a
All states with the same Rp fall on the lines parallel with the NCL.
ln Rp = ln ( p'y / p'a )
= ln p'y - ln p'a
Many features of soil behaviour, especially shear modulus and peak strength,
increase with increasing overconsolidation.
Back to Isotropic compression: state
Loading and
unloading
Vibration or compaction
(relevant to sands)
or creep
(relevant to clays)
Change of state can occur directly from A to B. Note that the yield
stress corresponding to B is larger than the yield stress corresponding to A.
Back to Isotropic compression: state
wet side of critical
(W on the graph)
vw > vc at stress p'
water content ww is larger than critical wc
· loose
· normally consolidated
or lightly overconsolidated
· compress during drained shear
dry side of critical
(D on the graph)
vd < vc at stress p'
water content wd is smaller than critical wc
· dense
· heavily overconsolidated
· dilate during drained shear
Back to Isotropic compression: state
Normalising parameters change the
current state to a normalised state so that all states with the same overconsolidation
ratio have the same value.
Equivalent specific volume
vl = va + l ln p'a
Equivalent pressure
ln p'e = ( N - va ) / l
Critical pressure
ln p'c = ( G - va
) / l
If A is on the wet side of critical
ve > G
p'a / p'c > 1
If A is on the dry side of critical
ve < G
p'a / p'c < 1
Back to Compression and swelling
One-dimensional
loading is applied in an oedometer and occurs in the ground beneath wide
foundations, embankments or excavations.
s'z = vertical effective stress
H = height or thickness
vertical strain = volumetric strain
ev = DH
/ Ho = De / (1+eo)
where Ho, eo and s'o
are initial values.
As the vertical stress s'z is raised and lowered the top of the sample settles or heaves, or the layer contracts or expands.
Note that the compression-swelling-recompression curve is similar to
that for isotropic compression, but the axes used are (s'z,
e) rather than (p', v).
Back to One-dimensional compression and swelling
For one-dimensional
compression and swelling there are simple relationships between the void
ratio and the logarithm of the vertical effective stress s'z.
First loading:
normal compression line (NCL)
OAD on the graph
e = eN - Cc log s'z
Unloading and reloading:
swelling-recompression line (SRL)
BC on the graph
e = ek - Cs log s'z
· eN, Cc and Cs are soil parameters
· ek and s'y
locate a particular swelling line
If the current stress s'o and
the history of loading and unloading are known, the current void ratio
can be calculated. e.g.
eo = eN - Cc log s'y
+ Cs (s'y - s'o
)
Back to One-dimensional compression: equations
The one-dimensional
stiffness modulus is the slope of the stress/strain curve:
M' = Ds'z / Dev
or
E'o = Ds'z / Dez
(since eh = 0)
The reciprocal of stiffness is compressibility. The one-dimensional coefficient of compressibility is the slope of the strain/stress curve:
mv = De / (Ds'z
(1+e))
= 1 / E'o
E'o and mv apply for the normal compression line
and for swelling and recompression lines, and depend on the current state,
on the history and on the increment of loading, so they are not soil constants.
Since mv varies with s'z,
its value is often quoted for s'z
= 100kPa.
Back to One-dimensional compression and swelling
If the current
state of soil is on the normal compression line it is said to be normally
consolidated. If the soil is unloaded it becomes overconsolidated.
Soil cannot usually be at a state outside the normal compression line unless it is bonded or structured.
At a state A the overconsolidation ratio is
Ro = s'y / s'a
(on NCL Ro = 1.0 and soil is normally consolidated).
Note: s'y is the point of intersection
of the swelling line through A and the NCL. This is usually, but not always,
close to the maximum past stress (see change of state).
Back to One-dimensional compression and swelling
During one-dimensional
loading and unloading the horizontal effective stress s'h
will change since the condition of zero horizontal strain (eh
= 0) is imposed.
The ratio Ko = s'h / s'z is known as the coefficient of earth pressure at rest.
Ko depends on
· the type of soil
· the overconsolidation ratio (Ro)
· the loading or unloading cycle
Approximations
normally consolidated soils:
Konc » 1 - sinf'c
overconsolidated soils:
Ko » Konc ÖRo
Back to One-dimensional compression and swelling
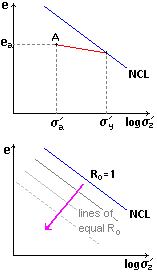The current state
of a soil is described by the stress s', the
void ratio e and the overconsolidation ratio Ro (for a complete
description the shear stress t' is required).
The state at A is given by any two of
ea , s'a , Ro
= s'y / s'a
All states with the same Ro fall on the lines parallel with the NCL.
log Ro = log ( s'y
/ s'a )
= log s'y - log s'a
Many features of soil behaviour, especially shear modulus and peak strength,
increase with increasing overconsolidation.
Back to One-dimensional compression: state
Loading and
unloading
Vibration or compaction
(relevant to sands)
or creep:
(relevant to clays)
Change of state can occur directly from A to B. Note that the yield
stress corresponding to B is larger than the yield stress corresponding
to A.
Back to One-dimensional compression: state
There is a critical
overconsolidation ratio which separates states in which the soil will either
compress or dilate during shear. This corresponds to the critical state
line CSL. Look at the possible voids ratios (e) that can occur at an effective
stress
s'a.
wet side of critical
(W on the graph)
ew > ec at stress s'
water content ww is larger than critical wc
· loose
· normally consolidated
or lightly overconsolidated
· compress during drained shear
dry side of critical
(D on the graph)
ed < ec at stress s'
water content wd is smaller than critical wc
· dense
· heavily overconsolidated
· dilate during drained shear
Back to One-dimensional compression: state
Normalising parameters change the
current state to a normalised state so that all states with the same overconsolidation
ratio have the same value.
Equivalent void ratio
el = ea + Cc log s'a
Equivalent stress
log s'e = ( eN - ea
) / Cc
Critical stress
log s'c = ( eG - ea
) / Cc
If A is on the wet side of critical
el > eG
s'a / s'c
> 1
If A is on the dry side of critical
el < eG
s'a / s'c
< 1
Back to Compression and swelling
Soils whose states
lie on the normal compression line (NCL) are normally consolidated.
There is a critical overconsolidation ratio that corresponds with the
critical state line (CSL).
A lightly overconsolidated soil has a state which lies above
the CSL.
A heavily overconsolidated soil has a state which lies below
the CSL.
States lying above the CSL are said to be on the wet side
of critical.
States lying below the CSL are said to be on the dry side
of critical.
In the diagrams: va > vb, and yet since the stress at B is greater, state B is on the wet side of critical, while state A is on the dry side of critical.
Back to Compression and swelling
Soils whose states
lie on the normal compression line (NCL) are normally consolidated.
There is a critical overconsolidation ratio that corresponds with the
critical state line (CSL).
A lightly overconsolidated soil has a state which lies
above
the CSL.
A heavily overconsolidated soil has a state which lies
below
the CSL.
States lying above the CSL are said to be on the wet side
of critical.
States lying below the CSL are said to be on the dry side
of critical.
In the diagrams: va > vb, and yet since the stress
at B is greater, state B is on the wet side of critical, while state A
is on the dry side of critical.
Back to Wet and dry states
A measure of the
initial state of a soil are the distances it lies at from the CSL, in terms
of either volume or stress. These distances are expressed as state parameters:
Stress state parameter
Ss = pa' / pc'
ln Ss = ln pa' - ln pc'
Volume state parameter
Sv = va - vc
The state parameters are related:
Sv = ln Ss
Normally consolidated state:
Sv = l ln Ss = 0
States on the wet side of critical:
Sv and ln Ss are positive
States on the dry side of critical:
Sv and ln Ss are negative
