Foundations
The foundation of a structure is in direct contact with the ground and transmits the load of the structure
to the ground. Foundations may be characterised as shallow (pad, strip or raft) or deep
(piles, piers or caissons). When designing foundations, two principal criteria must be satisfied:
Bearing capacity
There must be an adequate factor of safety
against collapse (plastic yielding in the soil and catastrophic settlement or rotation of the structure).
Settlement
Settlements at working loads must not cause damage, nor adversely affect the serviceability of the structure.
There are other considerations that may be relevant to specific soils, foundation types and surface conditions.
Foundations
Load-settlement behaviour
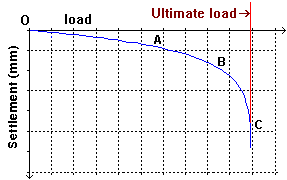 The application of a load on a foundation causes some settlement.
The three main stages of the load-settlement curve are:
The application of a load on a foundation causes some settlement.
The three main stages of the load-settlement curve are:
Relatively elastic vertical compression
(O-A) The load-settlement curve is almost straight.
Local shear failure
(B) Local yielding causes some upward and outward movement of the soil and results in slight surface heave.
General shear failure
(C) Large settlements are produced as plastic yielding is fully developed within the soil.
Bearing capacity failure can occur in three different modes: general shear failure, local shear failure, or
punching shear failure. Local or punching shear are characterised by relatively large settlements and the ultimate
bearing capacity is not clearly defined. In these cases settlement is the major factor in the foundation design.
Load-settlement behaviour
General shear failure
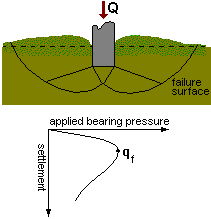 When a load (Q) is gradually applied on a foundation,
settlement occurs which is almost elastic to begin with. At the ultimate load, general shear failure
occurs when a plastic yield surface develops under the footing, extending outward and upward to the ground surface,
and catastrophic settlement and/or rotation of the foundation occurs. The load per unit area at this point is called
the ultimate bearing capacity (qf) of the foundation.
When a load (Q) is gradually applied on a foundation,
settlement occurs which is almost elastic to begin with. At the ultimate load, general shear failure
occurs when a plastic yield surface develops under the footing, extending outward and upward to the ground surface,
and catastrophic settlement and/or rotation of the foundation occurs. The load per unit area at this point is called
the ultimate bearing capacity (qf) of the foundation.
Load-settlement behaviour
Local shear failure
 In moderately compressible soils, and soils of medium relative density,
significant vertical settlement may take place due to local shear failure, i.e. yielding close to the
lower edges of the footing. The yield surfaces often do not reach the surface. Several yield developments may
occur accompanied by settlement in a series of jerks. The bearing pressure at which the first yield takes
place is referred to as the first-failure pressure (qf(1)) - the term first-failure load
(Qf(1)) is also used.
In moderately compressible soils, and soils of medium relative density,
significant vertical settlement may take place due to local shear failure, i.e. yielding close to the
lower edges of the footing. The yield surfaces often do not reach the surface. Several yield developments may
occur accompanied by settlement in a series of jerks. The bearing pressure at which the first yield takes
place is referred to as the first-failure pressure (qf(1)) - the term first-failure load
(Qf(1)) is also used.
Load-settlement behaviour
Punching shear failure
 In weak compressible soils, and soils of low relative density,
considerable vertical settlement may take place with the yield surfaces restricted to vertical planes
immediately adjacent to the sides of the foundation; the ground surface may be dragged down.
After the first yield has occured the load-settlement curve will steepen slightly, but remain fairly flat.
This is referred to as a punching shear failure.
In weak compressible soils, and soils of low relative density,
considerable vertical settlement may take place with the yield surfaces restricted to vertical planes
immediately adjacent to the sides of the foundation; the ground surface may be dragged down.
After the first yield has occured the load-settlement curve will steepen slightly, but remain fairly flat.
This is referred to as a punching shear failure.
Load-settlement behaviour
Factors affecting modes of failure
 According to experimental results from foundations resting on sands
(Vesic, 1973), the mode of failure likely to occur in any situation depends on the size of the foundation and
the relative density of the soil.
According to experimental results from foundations resting on sands
(Vesic, 1973), the mode of failure likely to occur in any situation depends on the size of the foundation and
the relative density of the soil.
- Other factors might be:
-
permeability: relating to drained/undrained behaviour
compressibility: similar to RD
shape: e.g. strips can only rotate one way
interaction between adjacent foundations and other structures
relative stiffnesses of soil and footing/structure
incidence and relative magnitude of horizontal loadings or moments
presence of stiffer or weaker underlying layers.
Foundations
Settlement
The are three components making up the final settlement quantity:
- Immediate settlement (ri)
- · elastic deformation with no change in water content
- · occurs rapidly during the application of load
- · quite small quantity in dense sands/gravels and stiff/hard clays
- Consolidation settlement (rc)
- · decrease in voids volume as porewater is squeezed out of the soil
- · occurs slowly according to the permeability
- · only significant in clays and silts
- Secondary settlement or creep (ra)
- · due to gradual changes in the particulate structure of the soil
- · occurs very slowly, long after consolidation is completed
- · most significant in soft organic soils and peats
Thus, final settlement, r = ri + rc + ra
Reliable predictions of settlement require a thorough assessment of ground conditions, including measurements of soil properties. Extensive ground investigations and statistically-reliable testing programmes can be expensive and time-consuming, and thus not economically viable for the routine design of shallow foundations.
Settlement
Total and differential settlement criteria
The principal undesirable effects of settlement in buildings are cracking due to angular distortion; tilting due to differential settlement and excessive downward displacement. The settlement of foundations must be limited to satisfy three main sets of criteria:
Cracking or tilting that affects visual appearance
· cracking damage can be related to the ease of repair
· a vertical tilt (w) of > 1/250 is unpleasantly noticeable
· horizontal dveviation of >1/100 and deflection/span ratos are also noticeable
Cracking or other damage that adversely affects serviceability
· cracking of wall and floor components can affect serviceability and be costly to repair
· differential displacements may affect the functionality of lifts, conveyors, cranes, internal traffic movement, aligment of drains, etc.
Damage that affects structural integrity or stability
· Angular distortion (D/L) in the foundation produces consequential distortion and increases in stresses in the structure above
· Structural damage is unlikely to occur if D/L is < 1/150
· Values of D/L > 1/1000 can cause cracking and overstressing.
Total and differential settlement criteria
Definitions of quantities
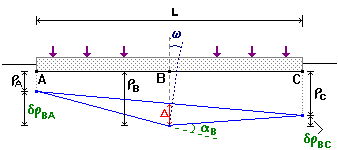
The following definitions and quantities have been suggested by Burland and Wroth (1975):
Settlement ( r or s): the downward displacement of a point in a foundation
Differential settlement (dr) the displacment of one point with respect to another
e.g drBA = displacement of B with respect to A = rB - rA
Angular strain ( a): the change in slope from horizontal at a point
Tilt angle (w): the vertical angle of displacement of a unit of structure
Relative deflection (D): maximum displacement between two points relative to a straight line drawn between them
Angular distortion (D/L): the ratio of the relative deflection between two points and the horizontal distance between them
Sagging occurs when the relative deflection is downward, i.e. D is +ve
Hogging occurs when the relative deflection is upward, i.e. D is -ve
Total and differential settlement criteria
Cracking and ease of repair
Jennings and Kerrich (1962) proposed a classification of damage due to the cracking based on the ease of repair.
| degree of damage | type of damage | crack width (mm) |
| 0 negligible |
Barely visible or none |
< 0.1 |
| 1 very slight |
Fine cracks repairable by normal decoration |
1-5 |
| 2 slight |
Cracks easily filled, may be visible externally.
Doors & windows stick slightly |
>5 |
| 3 moderate |
Cracks need raking out & filled by a mason
Doors & windows sticking Services fractured; water ingress |
5-15
(more than 3) |
| 4 severe |
Breaking out & replacing of masonry; floors sloping;
walls leaning/bulging; doors & windows not functioning;
floor beams displaced; services disrupted, serious water ingress |
15-25
(depends on number) |
| 5 very severe |
Rebuilding or major repair required; beams lose bearing;
walls require shoring;
danger of instability or collapse. |
>25
(depends on number) |
Settlements on clay
Imposed stress distribution below foundations
The distribution of stresses in the ground under a foundation due to applied loading is not uniform. Changes in vertical stress decrease with both depth and horizontal distance from the load; but can be predicted with reasonable accuracy using elasticity theory (and sometimes simpler approximate methods).
Imposed stress distribution below foundations
Boussinesq's solution
 According to Boussinesq (1885), the vertical stress Dsv in the ground due to a point load Q is
According to Boussinesq (1885), the vertical stress Dsv in the ground due to a point load Q is

where z is the depth below the load and r is the horizontal distance from the load.
Simple solutions are available for stresses below strip footings, below the centre of circular footings and below a corner of a rectangular footing. The latter can be used to calculate the stress at any point by dividing the rectangle into two or more rectangles and summing the stresses due to each part. For example, to find the stress under the centre of a (B x L) rectangular base, find the stress under the corner of a (1/2B x 1/2L) rectangle, then multiply by 4.
Imposed stress distribution below foundations
Stress below a circular foundation
The vertical stress at a depth z below the centre of circular base of radius R is
Dsv = q .Ic
where q is the bearing pressure and

The stress value below the centre is a maximum for a given depth. The expressions for stresses off-centre are much more complex. Over deep soil layers, the average value will be between 0.85 and 0.6 of the centre-line value according to the stiffness of the footing.
Imposed stress distribution below foundations
Stress below a strip foundation
 The vertical stress at a depth z below a uniformly loaded strip footing of width B=2b is
The vertical stress at a depth z below a uniformly loaded strip footing of width B=2b is
Dsv = q .Is
where q is the bearing pressure and
Is = [b + sin b.cos( b + 2 a) ] / p
Imposed stress distribution below foundations
Stress below a rectangular foundation
 The vertical stress at a depth z below the corner of a rectangular subject to uniform pressure is
The vertical stress at a depth z below the corner of a rectangular subject to uniform pressure is
Dsv = q. IR
where q is the bearing pressure and

Imposed stress distribution below foundations
Approximate methods
For settlement calculations (but not necessarily for other geotechnical problems), sufficient accuracy is usually obtained by assuming a simplified pressure distributuion. The two methods given below are in common use.
Tomlinson's method
Tomlinson suggests using an approximate pressure distribution
for small foundations on stiff clay:
Settlement, r = ( 1.5 B)
x ( 0.55 qn) x mv
- where
- B is the breadth of the foundation
- qn is the net bearing pressure
| 
|
2 : 1 distribution method
The vertical stress on horizontal planes is assumed to remain uniform, but decrease linearly with depth below the foundation, thus:
| For a strip footing: | 
|
| For a rectangular footing: | 
|
| where:
| qn = applied net bearing pressure
B = breadth,
L = length
z = depth from underside of footing
|
Settlement
Settlements on clays and silty clays
Settlements are time-dependent and may take several years to complete. The soil properties are obtained principally from laboratory tests. Relative proportions of final settlement that occur as immediate and consolidation settlement vary according to the stress history and state of the soil.
Soft normally consolidated clays and silts
ri » 0.1roed
where roed =
consolidation settlement from oedometer mv
The final settlement (excluding creep),
r = ri + roed = 1.1 roed
Stiff overconsolidated clays
Both immediate and consolidation settlement are incorporated in the oedometer-measured modulus.
Thus, final settlement, r = roed
Proportions:
ri » 0.5roed - 0.6roed
rc » 0.5roed - 0.4roed
Settlements on clays and silty clays
Calculating immediate settlement
The net immediate settlement is assumed to be due entirely to elastic volume change upon loading.
The following expression is based on elastic theory.
| Immediate settlement | 
|
| where
| qn = net bearing pressure
B = breadth of foundation
n = Poisson's ratio
Eu = undrained stiffness modulus
Ip = influence factor
|
Calculating immediate settlement
Typical values of Poisson's ratio
| Soil
| Poisson's ratio (n)
|
| Undrained saturated clays/silts | nu = 0.5 |
| Stiff sandy or silty clays | n´ = 0.2 - 0.4 |
| Medium to loose sands | n´ = 0.4 |
| Dense sands | n´ = 0.2 - 0.45 |
Calculating immediate settlement
Typical values of undrained stiffness
It is general practice to obtain values for Eu from undrained laboratory tests.
However, other empirical relationships can also be used:
From oedometer test results
The drained stiffness modulus,
E´ =
1/mv
and then
Eu = 1.5E´/(1 + n´)
where n´ = drained value of Poisson's ratio.
From undrained shear strength
In soils, stiffness moduli are strain-dependent. The strains associated with normal foundations at working loads are generally less than 0.1%. Some empirical relationships have been noted, for example, for London clay,
Eu /su = 150 to 500
Calculating immediate settlement
Typical values of influence factor
Influence factors Ip for vertical displacement due to elastic compression of a layer of semi-infinite thickness
| Shape |
Flexible |
Rigid |
| |
Centre |
Corner |
Average |
|
| Circle |
1.00 |
0.64 |
0.85 |
0.79 |
| Rectangle |
| |
| L/B = 1.0 |
1.122 |
0.561 |
0.946 |
0.82 |
| L/B = 1.5 |
1.358 |
0.679 |
1.148 |
1.06 |
| L/B = 2.0 |
1.532 |
0.766 |
1.300 |
1.20 |
| L/B = 3.0 |
1.783 |
0.892 |
1.527 |
1.42 |
| L/B = 4.0 |
1.964 |
0.982 |
1.694 |
1.58 |
| L/B = 5.0 |
2.105 |
1.052 |
1.826 |
1.70 |
| L/B = 10.0 |
2.540 |
1.270 |
2.246 |
2.10 |
| L/B = 100.0 |
4.010 |
2.005 |
3.693 |
3.47 |
Settlements on clays and silty clays
Calculating consolidation settlement
- The oedometer settlement of a soil layer can be calculated from:
roed = mv.Ds´.HL
where
mv = coefficient of volume compressibilty measured in an oedometer test
Ds´ = the average change in vertical effective stress in the layer
HL = thickness of the layer
In layered deposits, the sum of layer-settlements should be take down to a depth where
Ds´ < 0.1qn
Oedometer test results tend to overestimate the actual settlement; the following correction factors should be applied:
rc = mg.roed
where mg = a factor suggested by Skempton and Bjerrum (1957)
|
Type of clay |
mg |
|
Very sensitive; soft alluvial, estuarine and
marine clays |
1.0-1.2 |
|
Normally consolidated clay |
0.7-1.0 |
|
Overconsolidated clays,
e.g. London Clay, Weald, Kimmeridge, Oxford and Lias
clays.
|
0.5-0.7 |
|
Heavily overconsolidated clays,
e.g. Keuper Marl, glacial till
|
0.2-0.5 |
Calculating consolidation settlement
Typical values of volume compressibility
The values given below should be taken as guideline figures only, for preliminary design and first estimates; values based on reliable tests should be used in final design calculations.
|
Type of soil |
Degree of commpressibility |
mv
(m²/MN) |
|
Heavilly overconsolidated clays |
Very low compressibilty |
< 0.05 |
|
Overconsolidated clays |
Low compressibilty |
0.05 - 0.1 |
|
Weathered overconsolidated clays |
Medium compressibilty |
0.1 - 0.3 |
|
Normally consolidated clays |
High compressibilty |
0.3 - 1.5 |
|
Organic alluvial clays and silts; peats |
Very high compressibilty |
> 1.5 |
Settlement
Settlements on sands and gravels
Settlements on sands and gravels take place almost immediately. Obtaining undisturbed samples for laboratory testing is difficult. The soil properties are estimated from in situ test results.
Standard penetration test
Relationships have been suggested between N-values and the settlement; one exmaple is that of Burland and Burbidge (1985), a simplified version of which is:
Immediate settlement,

where qn´ = net effective bearing pressure
B = breadth of foundation
N =
average SPT N-value in the layer below of thickness B
Cone penetration test
For overconsolidated sands, estimates of E´ may be made from the measured cone resistance (qc):
When qc < 50 MN/m², E' - 5qc
When qc >= 50 MN/m², E' - 250 MN/m²
Pressuremeter tests
The shear modulus G is obtained from pressuremeter results.
Then, E´= 2G(1 + n´)
Foundations
Foundation design
Design is an iterative process. Designers use their experience to estimate the dimensions, then check whether the design is safe. If it is not safe, or the check indicated that it may be possible to make economies, then they modify the dimensions and repeat the calculations. For example:
Use presumed bearing values to obtain a first estimate of the size.
Calculate the ultimate bearing capacity (qf) at which collapse will occur.
Obtain the allowable bearing pressure from

Divide the design load by this allowable pressure to obtain a required area.
Select appropriate dimensions.
Calculate the likely settlement for this size of foundation.
Check that the predicted settlement due to this allowable bearing pressure is likely to be acceptable.
 The application of a load on a foundation causes some settlement.
The three main stages of the load-settlement curve are:
The application of a load on a foundation causes some settlement.
The three main stages of the load-settlement curve are: When a load (Q) is gradually applied on a foundation,
settlement occurs which is almost elastic to begin with. At the ultimate load, general shear failure
occurs when a plastic yield surface develops under the footing, extending outward and upward to the ground surface,
and catastrophic settlement and/or rotation of the foundation occurs. The load per unit area at this point is called
the ultimate bearing capacity (qf) of the foundation.
When a load (Q) is gradually applied on a foundation,
settlement occurs which is almost elastic to begin with. At the ultimate load, general shear failure
occurs when a plastic yield surface develops under the footing, extending outward and upward to the ground surface,
and catastrophic settlement and/or rotation of the foundation occurs. The load per unit area at this point is called
the ultimate bearing capacity (qf) of the foundation. In moderately compressible soils, and soils of medium relative density,
significant vertical settlement may take place due to local shear failure, i.e. yielding close to the
lower edges of the footing. The yield surfaces often do not reach the surface. Several yield developments may
occur accompanied by settlement in a series of jerks. The bearing pressure at which the first yield takes
place is referred to as the first-failure pressure (qf(1)) - the term first-failure load
(Qf(1)) is also used.
In moderately compressible soils, and soils of medium relative density,
significant vertical settlement may take place due to local shear failure, i.e. yielding close to the
lower edges of the footing. The yield surfaces often do not reach the surface. Several yield developments may
occur accompanied by settlement in a series of jerks. The bearing pressure at which the first yield takes
place is referred to as the first-failure pressure (qf(1)) - the term first-failure load
(Qf(1)) is also used. In weak compressible soils, and soils of low relative density,
considerable vertical settlement may take place with the yield surfaces restricted to vertical planes
immediately adjacent to the sides of the foundation; the ground surface may be dragged down.
After the first yield has occured the load-settlement curve will steepen slightly, but remain fairly flat.
This is referred to as a punching shear failure.
In weak compressible soils, and soils of low relative density,
considerable vertical settlement may take place with the yield surfaces restricted to vertical planes
immediately adjacent to the sides of the foundation; the ground surface may be dragged down.
After the first yield has occured the load-settlement curve will steepen slightly, but remain fairly flat.
This is referred to as a punching shear failure. According to experimental results from foundations resting on sands
(Vesic, 1973), the mode of failure likely to occur in any situation depends on the size of the foundation and
the relative density of the soil.
According to experimental results from foundations resting on sands
(Vesic, 1973), the mode of failure likely to occur in any situation depends on the size of the foundation and
the relative density of the soil.

 According to Boussinesq (1885), the vertical stress Dsv in the ground due to a point load Q is
According to Boussinesq (1885), the vertical stress Dsv in the ground due to a point load Q is


 The vertical stress at a depth z below a uniformly loaded strip footing of width B=2b is
The vertical stress at a depth z below a uniformly loaded strip footing of width B=2b is The vertical stress at a depth z below the corner of a rectangular subject to uniform pressure is
The vertical stress at a depth z below the corner of a rectangular subject to uniform pressure is





